Minimum APC Difference Worth Detecting in Joinpoint Fitting
In some situations Joinpoint may determine that there are one or more pairs of segments where the difference in slopes (i.e. difference in the Annual Percent Change) between some consecutive segments is quite small. For cancer trends, this tends to occur in the larger cancer sites where there is increased statistical power to detect small differences. Often the analyst is focused on trying to interpret only larger differences, and would like to eliminate joinpoints where the APC difference falls below a specified threshold because they are too small to be of practical importance and/or may be difficult to interpret It is important to note that this is a subjective criteria that overlays the statistical criteria which is applied first. We call this procedure Minimum APC Difference Worth Detecting (MADWD).
The user enters a minimum APC difference worth detecting as a minimum percentage point difference (Min PPD). For cancer incidence and mortality trends we have generally not found any APC differences less than 0.25 percentage points. A reasonable choice might be a Min PPD of 0.5 percentage points or 0.75 percentage points, although it is completely subjective and depends on the context of the analysis. The Min PPD should generally be selected before analyzing the data. This will guard against an analyst post hoc systematically varying the MIN PPD until they obtain results which conform with pre-conceived notions of what the trends should look like.
The procedure first uses the specified statistical criteria to determine the number of joinpoints. Each pair of segments is then tested to determine if the APC difference is less than the specified cutoff level. If any pairs of segments fails (i.e. APC difference less than the specified level) then a new joinpoint model with one less segment is fit, and that model is tested to see if all segments pass the MADWD criteria. This process is continued until we find the joinpoint model where all consecutive segments pass the criteria.
More technically, consider the joinpoint regression model with κ + 1 segments: for i = 1,...,n,
\(\Large y_i = log(r_i) = \beta_0 + \beta_1x_i + \delta_1(x - \tau_1)^+ + \cdots + \delta_k(x - \tau_k)^+\Large\)
where a+ = max(a,0) and κ is the unknown number of joinpoints. Define the APC difference between the j-th and (j + 1)-st segments as
\(\|APC_{j+1} - APC_j \| = \left\{ \stackrel{ \ \ 100\|e^{\beta_1 + \delta_1} - e^{\beta_1} \| \approx \| \delta_1\| \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ for \ j = 1; \ \ \ \ \ \ \ \ \ \ }{100\|e^{\beta_1} + \sum {}_{l=1}^{j} \delta_l - e^{\beta_1} + \sum {}_{l=1}^{j-1} \delta_l \| \approx \| \delta_j\| \ \ \ \ \ \ for \ j = 2,...,\kappa}\right\}\)
\(\Large \left| APC_j+1 - APC_j\right| = \left\{ \right\} \Large\)
and we estimate it as
\(\ d_{j,j+1} = \left\{ \stackrel{ \ \ 100\|e^{\hat{\beta_1} + \hat{\delta_1}} - e^{\hat{\beta_1}} \| \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ for \ j = 1; \ \ \ \ \ \ \ \ \ \ }{100\|e^{\hat{\beta_1}} + \sum {}_{l=1}^{j} \hat{\delta_l} - e^{\hat{\beta_1}} + \sum {}_{l=1}^{j-1} \hat{\delta_l} \| \ \ \ \ \ \ for \ j = 2,...,\hat{\kappa}}\right\}\)
| Step 1. | Set the MADWD, say at ψ. |
| Step 2. | For each \(k = 0,...,\hat{\kappa},\) consider the best model fitted by Joinpoint. |
| Step 3. | For \(k = \hat{\kappa} (> 0),\) examine if all the adjacent segments meet the MADWD criteria. That is, check if \(d_{j,j+1} \geq \psi\) for all j = 1,...,k. |
| Step 4. | If k = 0 or all the neighboring segments meet the MADWD criteria, then stop. |
| Step 5. | If there are at least one neighboring segments not meeting the MADWD criteria, reduce k to \(\hat{\kappa} - 1\) and repeat Steps 3-5. |
Example
Below is an example of the final selected model for US mortality 1975-2016 for all malignant cancers, all races, male, all ages made from a Joinpoint analysis not using the MADWD criteria. A 4 joinpoint model was selected, but some of the changes in the APC between consecutive segments are small.
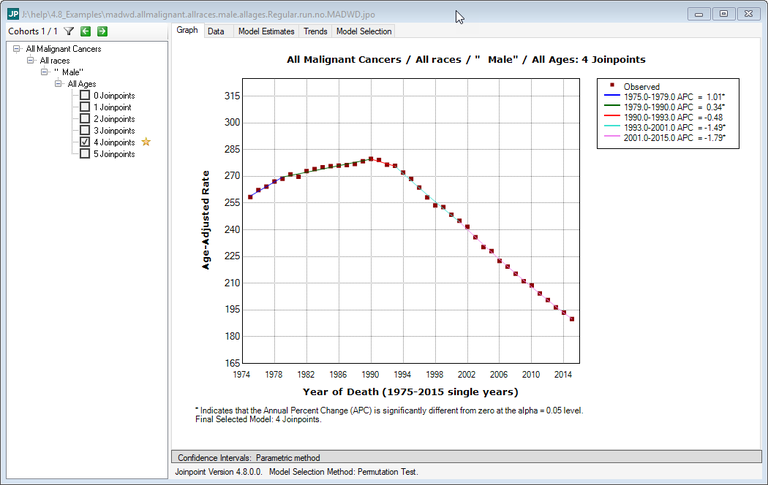
Now running the same session again using MADWD with a Minimum Percentage Point Difference (Min PPD) set to 0.5, we get the following:
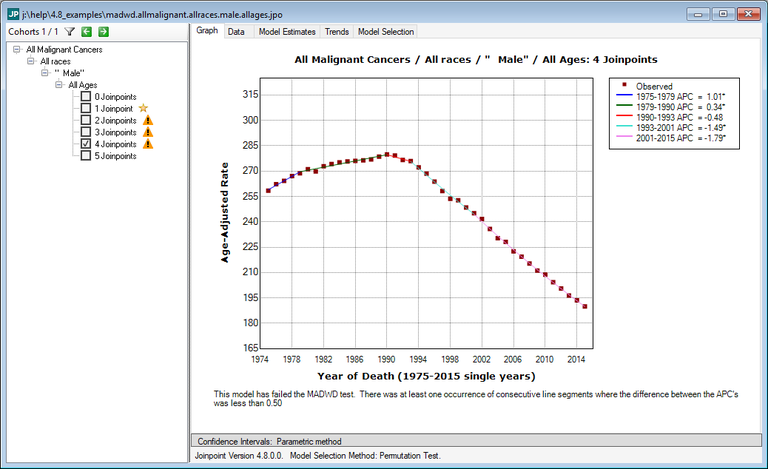
The 4 Joinpoint model failed the MADWD test because the percentage point difference between the 1993-2001 and 2001-015 segments is 0.30.

Below is the fit using 3 joinpoints.
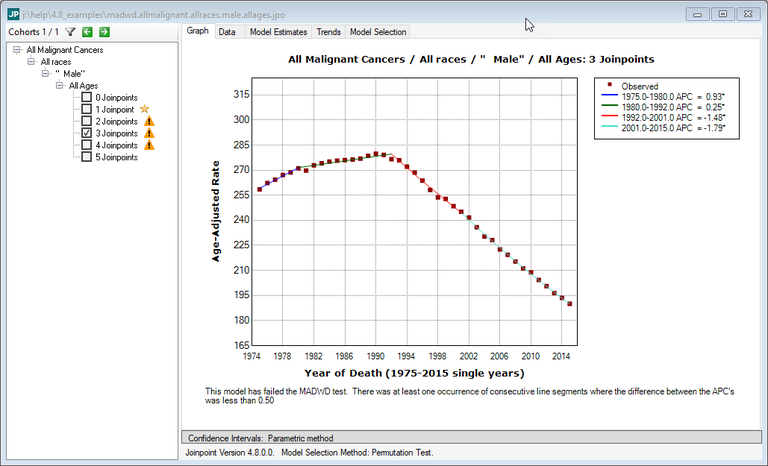
The 3 Joinpoint model failed the MADWD test because the percentage point difference between the 1992-2001 and 2001-2015 segments is 0.31.

Below is the fit using 2 joinpoints.
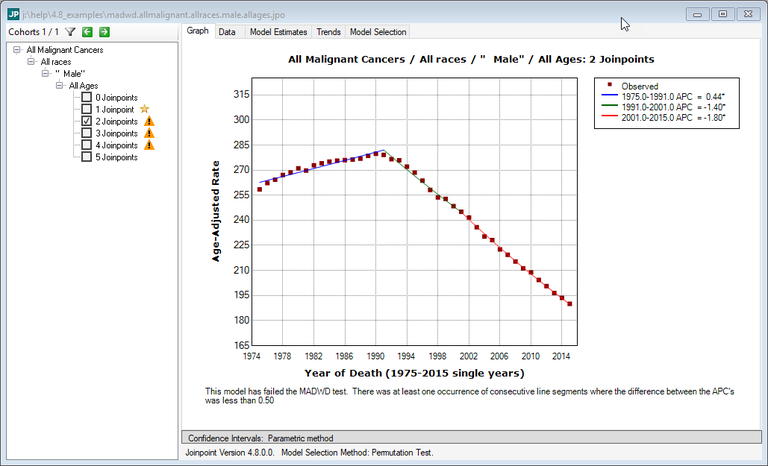
The 2 Joinpoint model failed the MADWD test because the percentage point difference between the 1991-2001 and 2001-2015 segments is 0.40.

Below is the fit using 1 joinpoint.
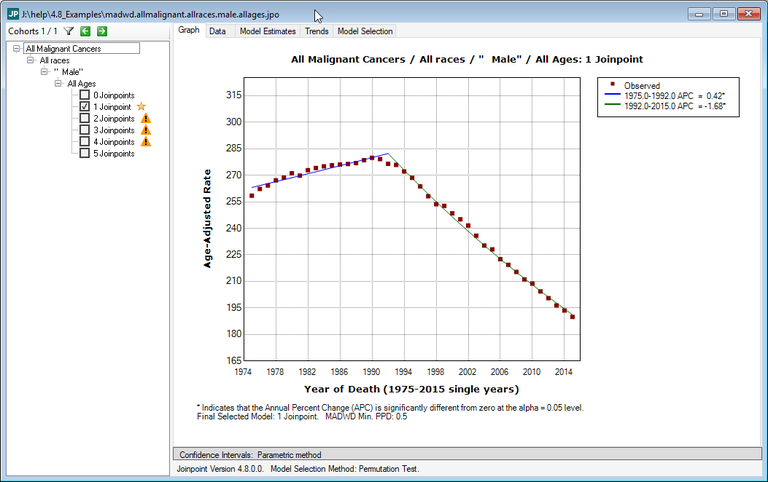
The one joinpoint model passes the MADWD test.

Table
For any MADWD analysis, a table indicating the MADWD tests conducted will be displayed on the Model Selection tab. The summary table for this MADWD analysis is shown below:

It is important to note the Min PPD is a subjective criteria which overlays the statistical criteria that is applied first. It is also generally important that the analyst does not keep modifying the Min PPD criteria after viewing results until they obtain a result which meets some preconceived notion of what the trends should look like.