CP*Trends–Interpreting Trend Plots
For every combination of incidence or mortality, sex, and a specified cancer site, two graphs are displayed. The first graph shows rates by age with birth cohort as the x-axis, and the second shows rates by age with calendar year as the x-axis. This means that in the first graph the rates for a person born in a specific year (e.g. 1935) are directly above each other as they age, while in the second graph the rates occurring in a specific calendar year (e.g. 1980) are directly above each other. The same rates are displayed in both graphs, but are just shifted. Because rates generally change across age groups in terms of percentage increases rather than in arithmetic increases, the y axis is displayed on a log scale, which also more conveniently shows a wide range of rates on a single graph.
If birth cohort factors are driving the changes in the rates, then lines on the birth cohort graph will be close to parallel, indicating that everyone born in a later or earlier birth cohort have age-specific rates a fixed percent higher or lower than a selected index cohort. By contrast, if calendar year factors are driving the changes in the rates, then the lines on the period graph will be close to parallel, indicating that people in a later or earlier calendar year will have age-specific rates a fixed percent higher lower than a selected index calendar year.
Non-Identifiability of Linear Trends
Due to the relationships between age, birth cohort and period (i.e. birth year + age = calendar year), if the trends are linear (on a log scale) then the lines are straight and parallel on both the age-cohort graph and the age-period graph (see Figure 1 below). This means that without any curvature to the lines, it is impossible to determine whether the factors associated with changes in rates over time are driven by factors associated with birth cohort or calendar year. The combined linear effect is sometimes called “drift”, indicating that the rates are “drifting” in a linear way, but it is not possible to disentangle whether the underlying cause of this drift is primarily period or cohort.
Curvature
When the trends show curvature, then parallelism on one graph will not yield parallelism on the other. The following figures show examples of curvature by period (Figure 2), cohort (Figure 3), or both (Figure 4). Table 1 shows the corresponding C-P Scores and % Deviance Explained by Period and Cohort for each of the figures.
| Figure | C-P Score | % Deviance Explained by Period and Cohort |
|---|---|---|
| 1 | Close to 0 | Close to 0% |
| 2 | Close to -1 | Close to 100% |
| 3 | Close to 1 | Close to 100% |
| 4 | Between +/- 1 | Close to 100% |
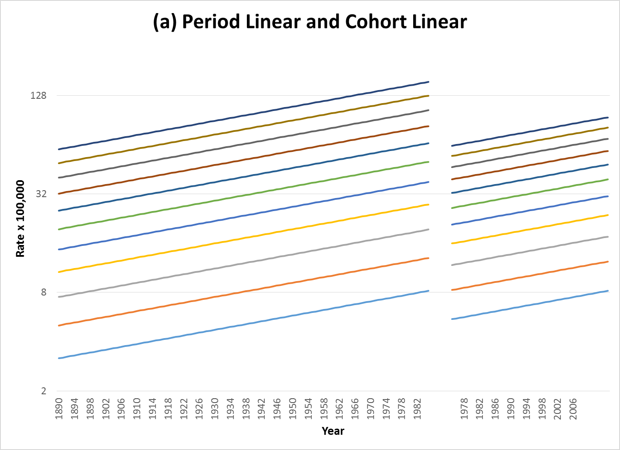
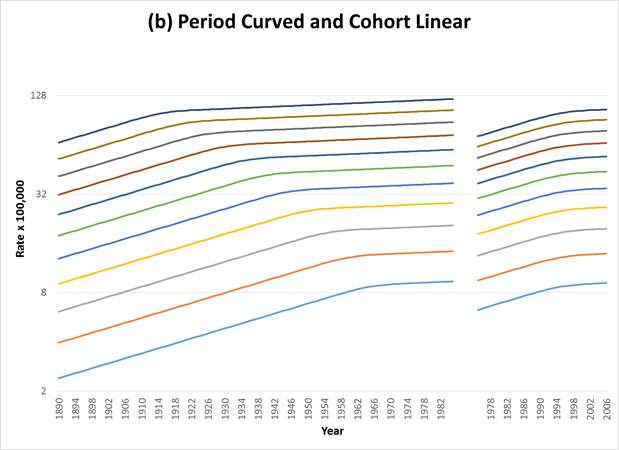
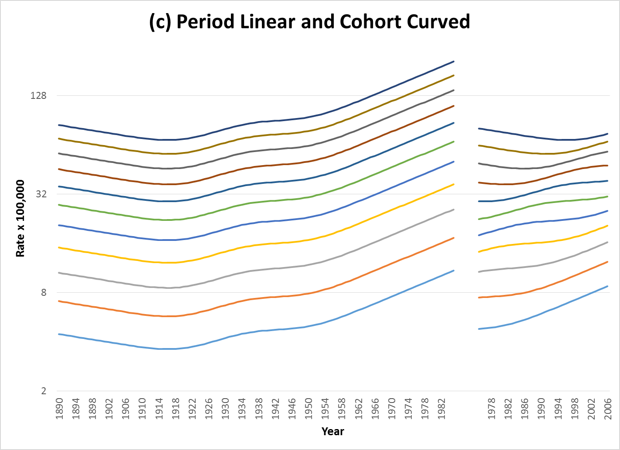
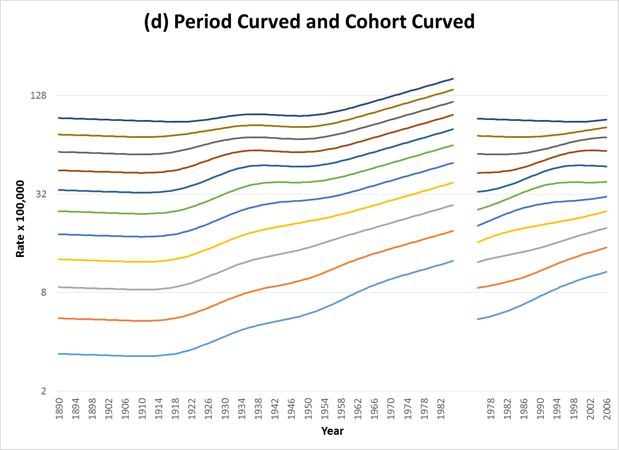
Because data are only available for a specified range of period, not all ages are represented in each cohort. In this case the figure will appear as follows:
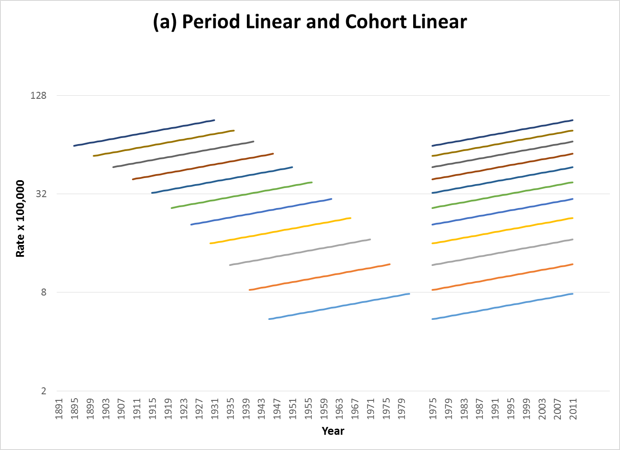
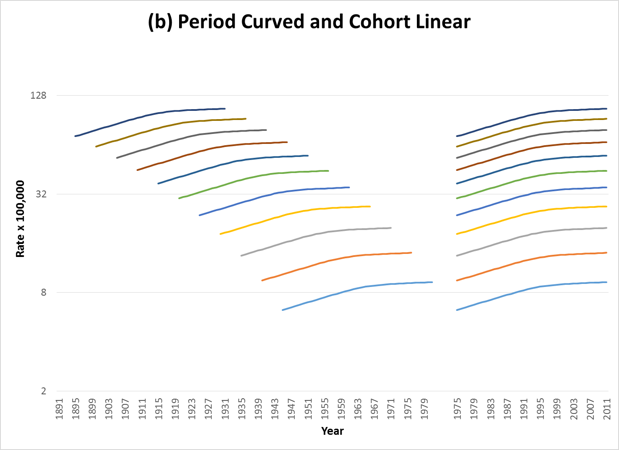
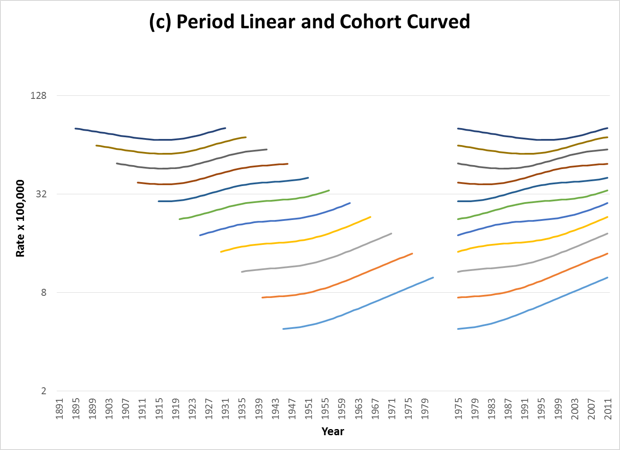
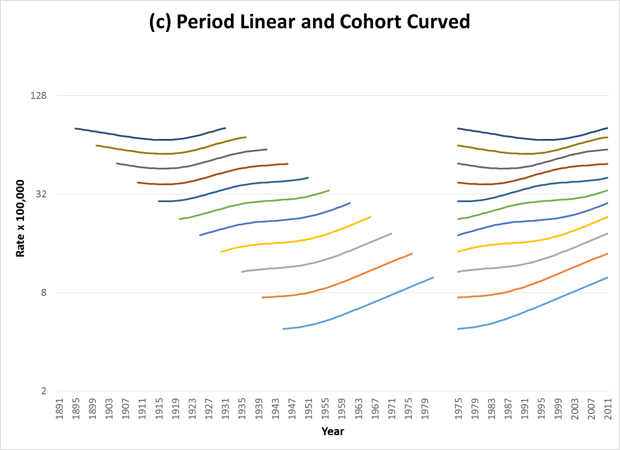
To visualize parallelism, one must consider segments of the lines that are directly above each other in the cohort graphs. One can see that in these examples, the representation of parallelism is identical to that in the previous set of graphs.
