CanSurv Survival Models

Denote the survival time of a cancer patient by T and the survival function by S(t)=Pr(T>t). The following models for S(t) are implemented by CanSurv.

Standard Parametric Survival Models

Four standard parametric survival models used in CanSurv are lognormal(LN), loglogistic(LN), Weibull(WB) and Gompertz (GP). Their survival functions for uncured patients (called latency distribution) are:

where μ and σ are the location and scale parameters in the parameterization for the LN, LL, and WB distributions. The parameters (μ, σ) may depend on covariates x, e.g.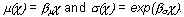

Cox Proportional Hazards (PH) Model

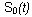The Cox proportional hazards model assumes that , where the baseline survival function is unspecified.

Mixture Cure Survival Models

The mixture cure survival model used in CanSurv is a two component (binary) mixture cure (Boag, 1949; Farewell, 1992) with cure fraction c:

where G(t | μ, σ) is a proper survival function. The parameter c, as well as (μ, σ), may depend on covariates x, e.g., . If G is a parametric function, the cure fraction is estimated by extrapolated the survival function beyond the observed data. If G is the semi-parametric Cox model, the cure fraction is defined as the proportion of survival after the last event time.

A mixture cure model with power function has been used in estimating the completeness index of cancer prevalence (Capocaccia and De Angelis, 1997):

where the power function δ may depend on x as . When δ=1, this model reduces to binary mixture cure model. However when power function δ is used, as least one covariate should be included in δ; also if a covariate is already included in δ, it cannot be used for (c, μ, σ).

CanSurv or SAS/Splus?

Many standard statistical softwares, e.g., SAS, Splus, Stata, etc, are available for survival analysis, and most of them fit standard survival models to data from clinical studies, i.e., cause-specific survival data with continuous survival times. CanSurv is specifically designed for population-based survival data, which are usually grouped into life tables and the measure of net survival is relative survival. Generally, if one wants to fit standard survival models without cure to cause-specific survival data, SAS or Splus are appropriate. Below we list the appropriate statistical procedures or functions depending on the survival data type.

Cause-specific survival data:

The standard parametric models can be fitted by PROC LIFEREG in SAS or survreg in Splus. The Cox proportional hazards model can be fitted by PROC PHREG in SAS or coxph in Splus. Note that the mixture cure models cannot be fitted by SAS or Splus.

Relative survival data:

Neither SAS nor Splus can be used to fit survival models to relative survival data. The only exception is that PROC GENMOD can be used to fit Cox proportional hazards model to grouped relative survival data (Hakulinen and Tenkanen, 1987). CanSurv is developed specifically for analyzing relative survival data. It can fit both standard survival models and mixture cure survival models to grouped survival data.